
|
Tim Hoffmann, Jannik Steinmeier, and Gudrun Szewieczek.
Discrete curve theory in space forms: planar elastic and
area-constrained elastic curves, 2025.
[ bib |
arXiv ]
We propose a notion of discrete elastic and area-constrained elastic curves in 2-dimensional space forms. Our definition extends the well-known discrete Euclidean curvature equation to space forms and reflects various geometric properties known from their smooth counterparts. Special emphasis is paid to discrete flows built from Bäcklund transformations in the respective space forms. The invariants of the flows form a hierarchy of curves and we show that discrete elastic and constrained elastic curves can be characterized as elements of this hierarchy. This work also includes an introductory chapter on discrete curve theory in space forms, where we find discrete Frenet-type formulas and describe an associated family related to a fundamental theorem.
|
|
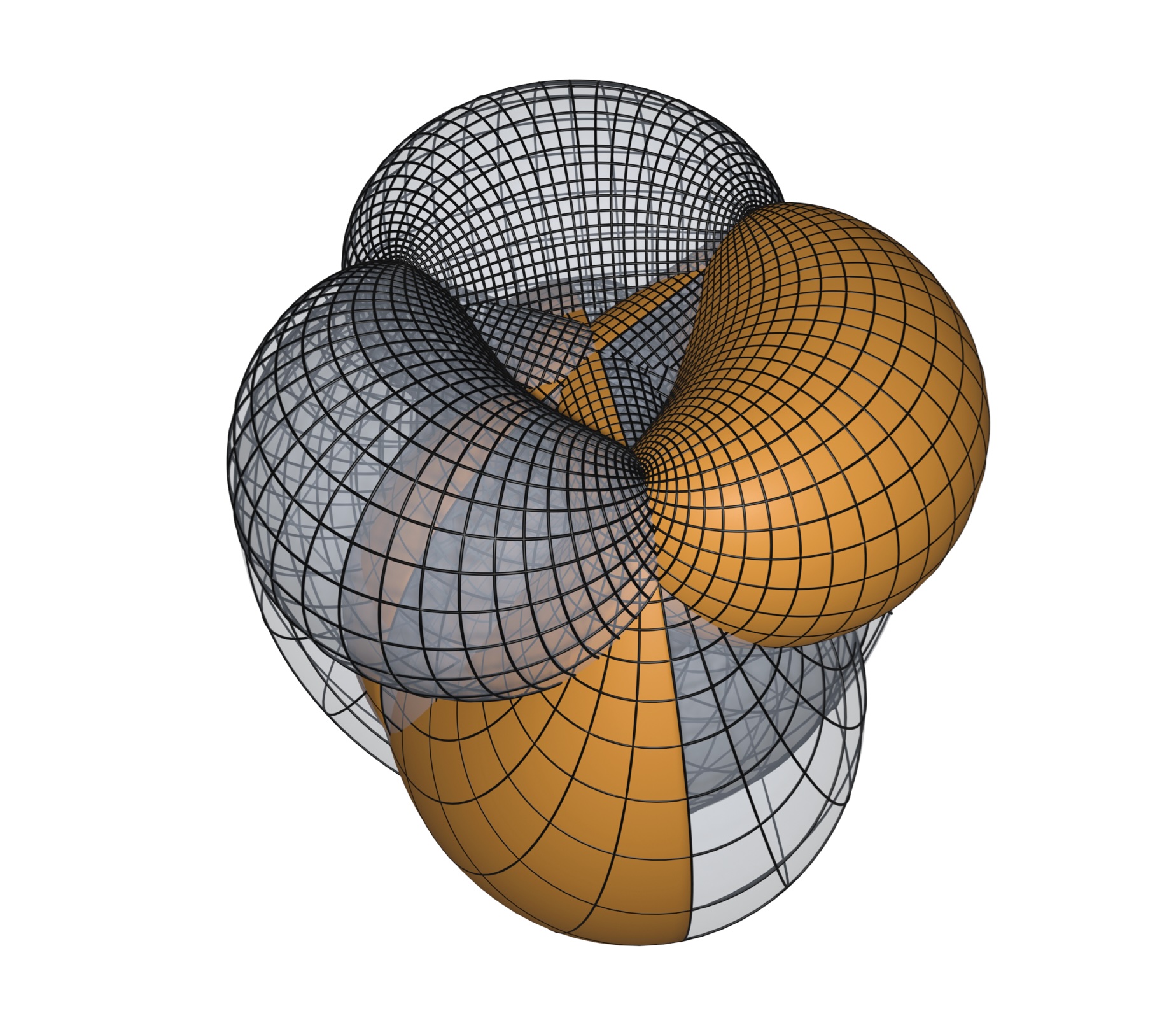
Alexander I. Bobenko, Tim Hoffmann, and Andrew O. Sageman-Furnas.
Isothermic tori with one family of planar curvature lines and area
constrained hyperbolic elastica, 2024.
[ bib |
arXiv ]
In 1883, Darboux gave a local classification of isothermic surfaces with one family of planar curvature lines using complex analytic methods. His choice of real reduction cannot contain tori. We classify isothermic tori with one family of planar curvature lines. They are found in the second real reduction of Darboux's description. We give explicit theta function formulas for the family of plane curves. These curves are particular area constrained hyperbolic elastica. With a Euclidean gauge, the Euler--Lagrange equation is lower order than expected. In our companion paper (arXiv:2110.06335) we use such isothermic tori to construct the first examples of compact Bonnet pairs: two isometric tori related by a mean curvature preserving isometry. They are also the first pair of isometric compact immersions that are analytic. Additionally, we study the finite dimensional moduli space characterizing when the second family of curvature lines is spherical. Isothermic tori with planar and spherical curvature lines are natural generalizations of Wente constant mean curvature tori, discovered in 1986. Wente tori are recovered in a limit case of our formulas.
|
|
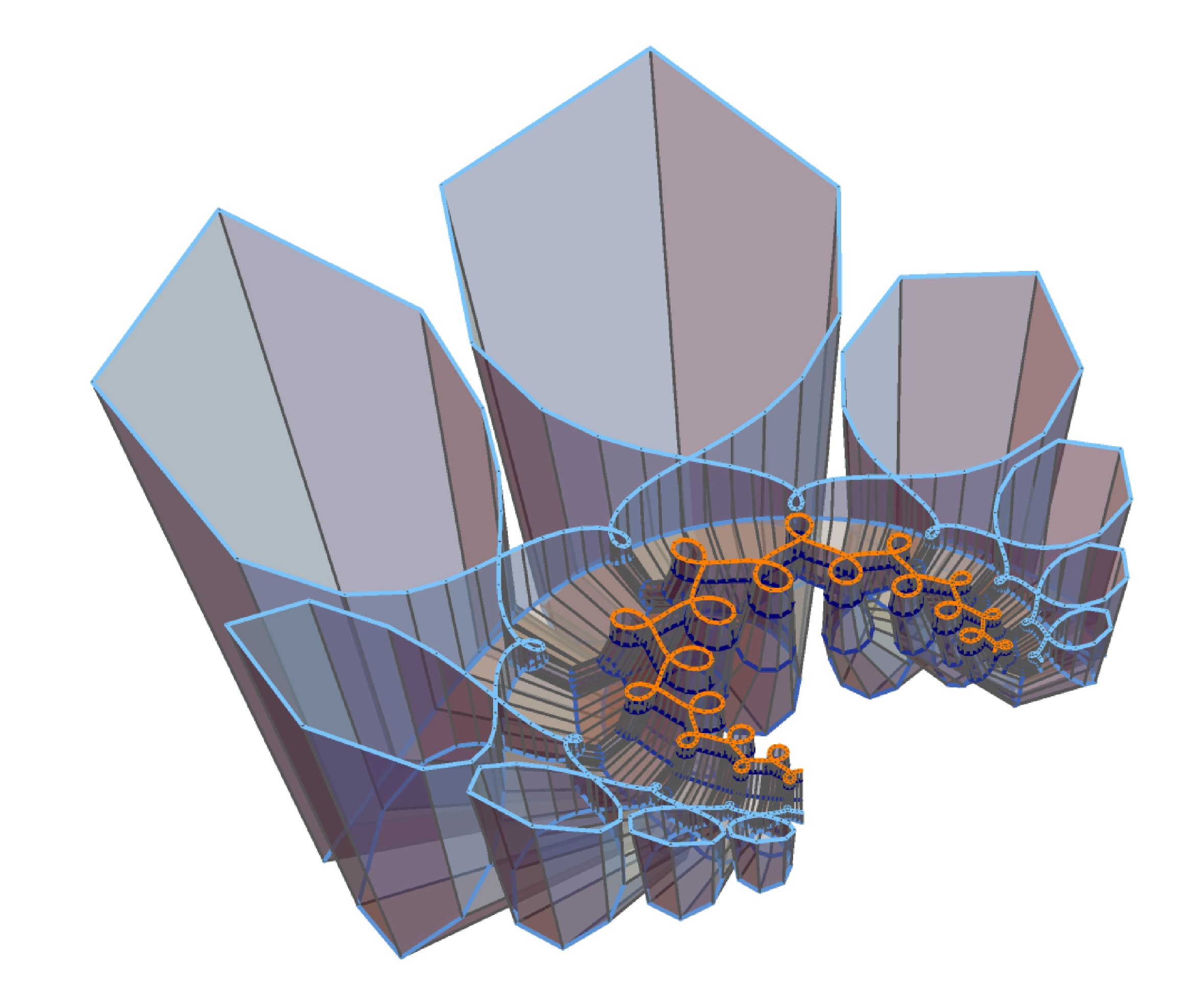
Tim Hoffmann and Gudrun Szewieczek.
Isothermic nets with spherical parameter lines from discrete
holomorphic maps, 2024.
[ bib |
arXiv ]
It is proven that discrete isothermic nets with a family of planar or spherical lines of curvature are obtained from special discrete holomorphic maps via lifted-folding. In particular, this novel approach provides an efficient way to generate discrete isothermic topological tori composed of fundamental pieces from discrete periodic holomorphic maps.
|
|
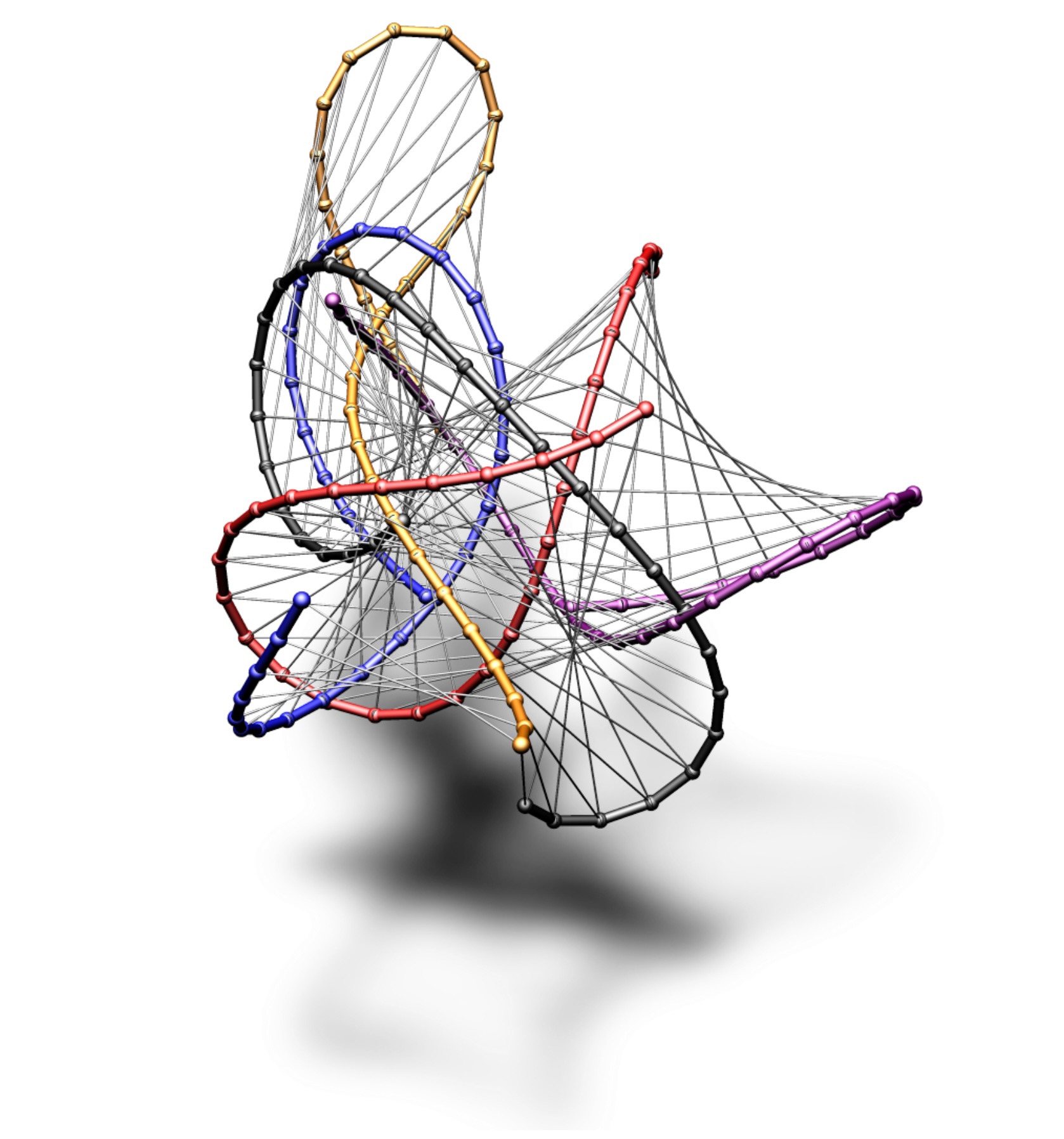
Jannik Steinmeier Tim Hoffmann, Andrew O. Sageman-Furnas.
Skew parallelogram nets and universal factorization, 2024.
[ bib |
arXiv ]
We obtain many objects of discrete differential geometry as reductions of skew parallelogram nets, a system of lattice equations that may be formulated for any unit associative algebra. The Lax representation is linear in the spectral parameter, and paths in the lattice give rise to polynomial dependencies. We prove that generic polynomials in complex two by two matrices factorize, implying that skew parallelogram nets encompass all systems with such a polynomial representation. We demonstrate factorization in the context of discrete curves by constructing pairs of Bäcklund transformations that induce Euclidean motions on discrete elastic rods. More generally, we define a hierarchy of discrete curves by requiring such an invariance after an integer number of Bäcklund transformations. Moreover, we provide the factorization explicitly for discrete constant curvature surfaces and reveal that they are slices in certain 4D cross-ratio systems. Encompassing the discrete DPW method, this interpretation constructs such surfaces from given discrete holomorphic maps.
|

|
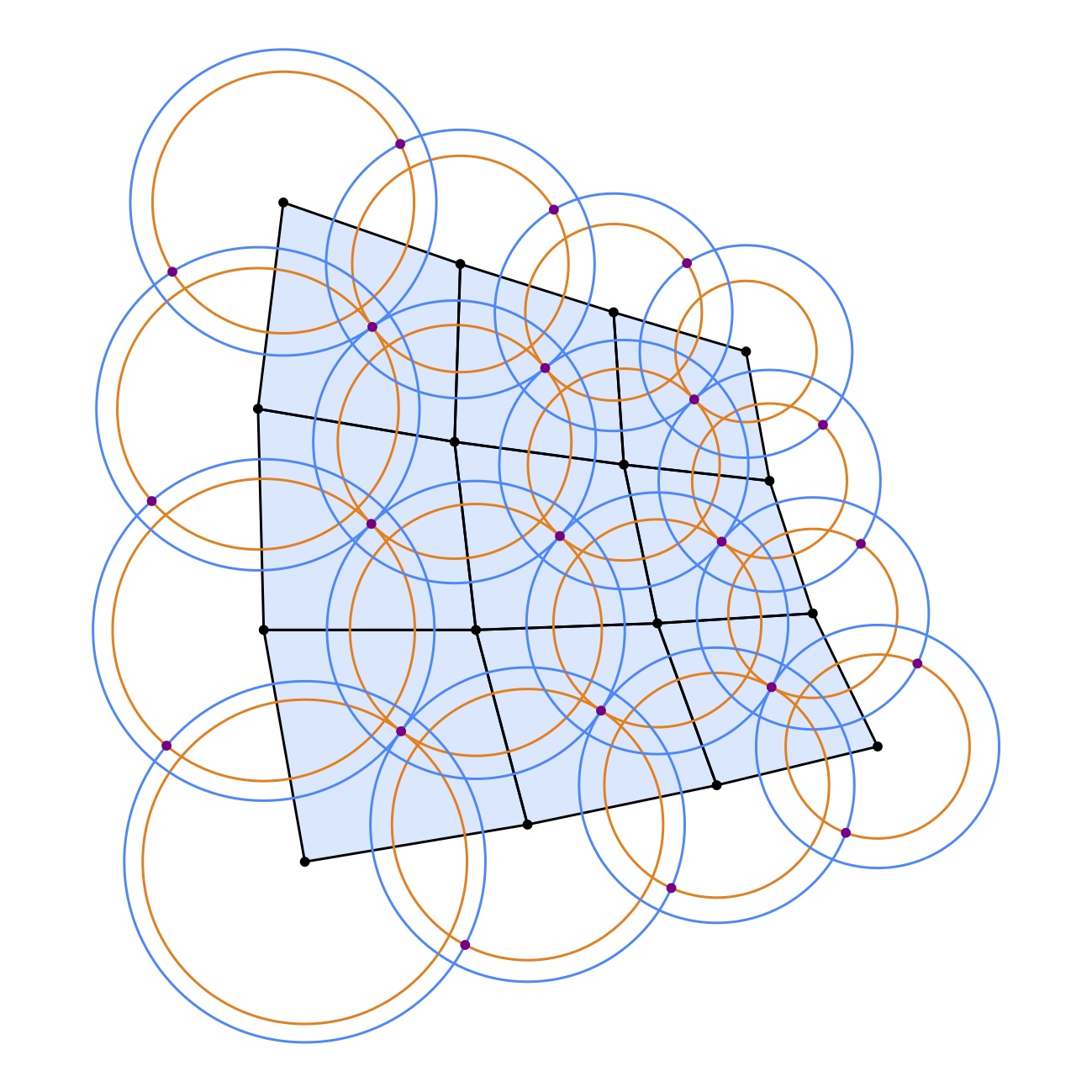
A. I. Bobenko, T. Hoffmann, and N. Smeenk.
Constant mean curvature surfaces from ring patterns: Geometry from
combinatorics, 2024.
[ bib |
arXiv ]
We define discrete constant mean curvature (cmc) surfaces in the three-dimensional Euclidean and Lorentz spaces in terms of sphere packings with orthogonally intersecting circles. These discrete cmc surfaces can be constructed from orthogonal ring patterns in the two-sphere and the hyperbolic plane. We present a variational principle that allows us to solve boundary value problems and to construct discrete analogues of some classical cmc surfaces. The data used for the construction is purely combinatorial - the combinatorics of the curvature line pattern. In the limit of orthogonal circle patterns we recover the theory of discrete minimal surfaces associated to Koebe polyhedra all edges of which touch a sphere. These are generalized to two-sphere Koebe nets, i.e., nets with planar quadrilateral faces and edges that alternately touch two concentric spheres.
|
|
Alexander I. Bobenko, Tim Hoffmann, and Thilo Rörig.
Orthogonal ring patterns in the plane.
Geometriae Dedicata, 218(11), 2023.
[ bib |
arXiv ]
We introduce orthogonal ring patterns consisting of pairs of concentric circles generalizing circle patterns. We show that orthogonal ring patterns are governed by the same equation as circle patterns. For every ring pattern there exists a one parameter family of patterns that interpolates between a circle pattern and its dual. We construct ring patterns analogues of the Doyle spiral, Erf and zα
functions. We also derive a variational principle and compute ring patterns based on Dirichlet and Neumann boundary conditions.
|

|
Floor Verhoeven, Amir Vaxman, Tim Hoffmann, and Olga Sorkine-Hornung.
Dev2pq: Planar quadrilateral strip remeshing of developable surfaces.
ACM Transactions on Graphics (TOG), 41(3):29:1--18, 2022.
[ bib |
arXiv ]
We introduce an algorithm to remesh triangle meshes representing developable surfaces to planar quad dominant meshes. The output of our algorithm consists of planar quadrilateral (PQ) strips that are aligned to principal curvature directions and closely approximate the curved parts of the input developable, and planar polygons representing the flat parts of the input that connect the PQ strips. Developable PQ-strip meshes are useful in many areas of shape modeling, thanks to the simplicity of fabrication from flat sheet material. Unfortunately, they are difficult to model due to their restrictive combinatorics. Other representations of developable surfaces, such as arbitrary triangle or quad meshes, are more suitable for interactive freeform modeling but generally have non-planar faces or are not aligned to principal curvatures. Our method leverages the modeling flexibility of non-ruling-based representations of developable surfaces while still obtaining developable, curvature-aligned PQ-strip meshes. Our algorithm optimizes for a scalar function on the input mesh, such that its isolines are extrinsically straight and align well to the locally estimated ruling directions. The condition that guarantees straight isolines is non-linear of high order and numerically difficult to enforce in a straightforward manner. We devise an alternating optimization method that makes our problem tractable and practical to compute. Our method works automatically on any developable input, including multiple patches and curved folds, without explicit domain decomposition. We demonstrate the effectiveness of our approach on a variety of developable surfaces and show how our remeshing can be used alongside handle-based interactive freeform modeling of developable shapes.
|
|
Tim Hoffmann, Shimpei Kobayashi, and Zi Ye.
Discrete constant mean curvature surfaces on general graphs.
Geometriae Dedicata, 216(71), 2022.
[ bib |
arXiv ]
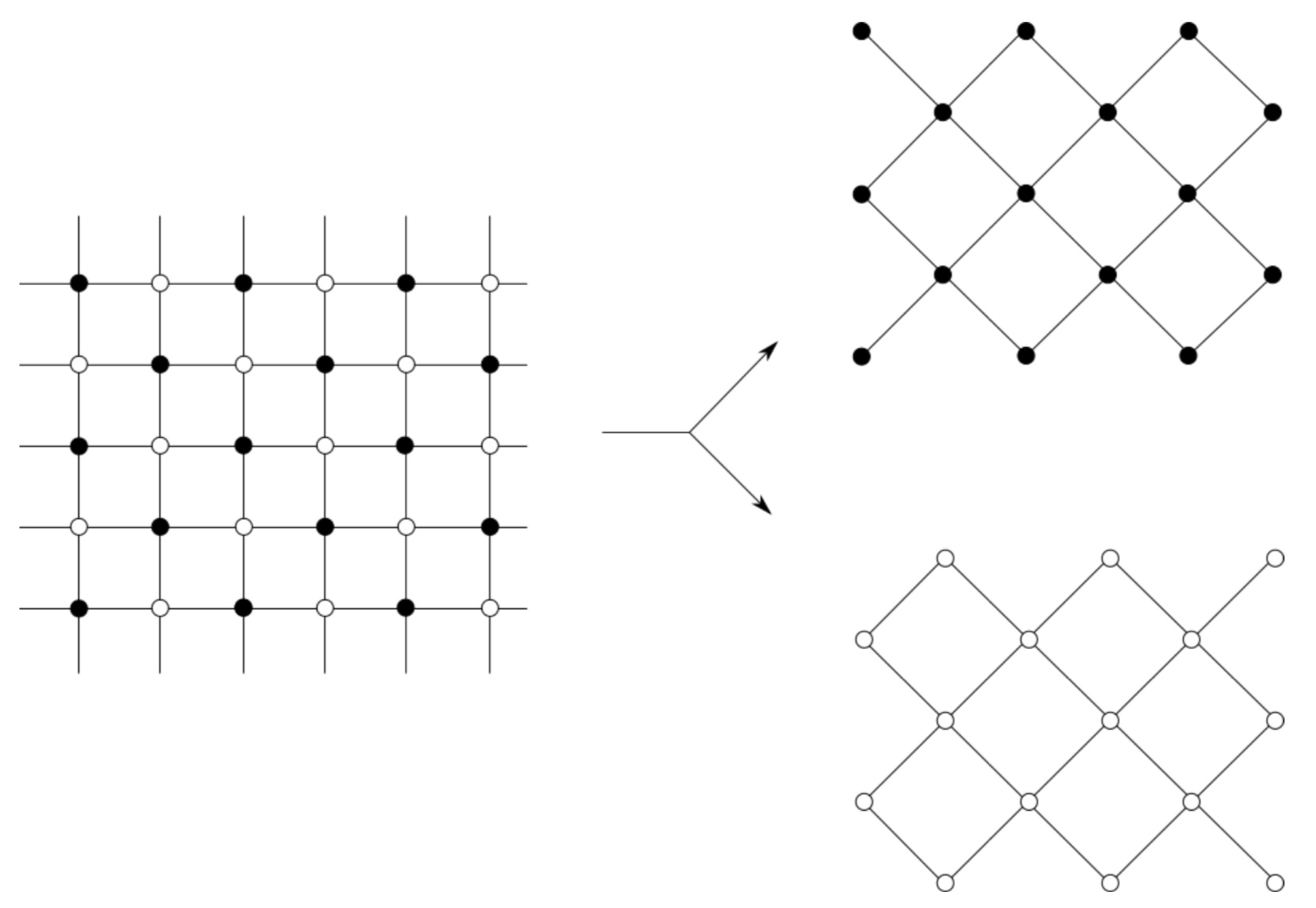
The contribution of this paper is twofold. First, we generalize the definition of discrete isothermic surfaces. Compared with the previous ones, it covers more discrete surfaces, e.g., the associated families of discrete isothermic minimal and non-zero constant mean curvature (CMC in short) surfaces, whose counterpart in smooth case are isothermic surfaces. Second, we show that the discrete isothermic CMC surfaces can be obtained by the discrete holomorphic data (a solution of the additive rational Toda system) via the discrete generalized Weierstrass type representation.
|
|
Tim Hoffmann, Wolfgang Schief, and Jannik Steinmeier.
On discrete conjugate semi-geodesic nets.
International Mathematics Research Notices, 02 2021.
[ bib |
DOI ]
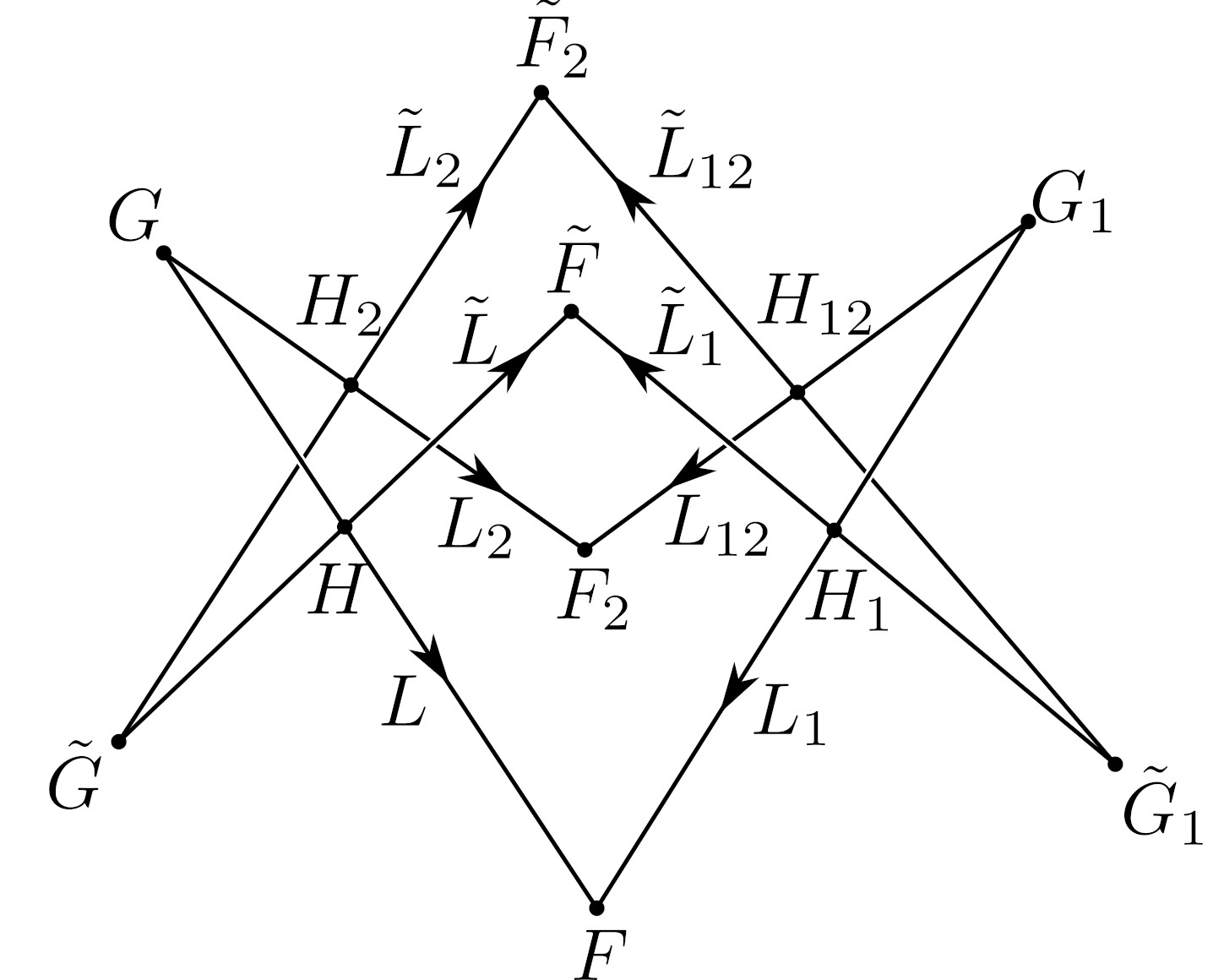
We introduce two canonical discretizations of nets on generic surfaces, which consist of an one-parameter family of geodesics and its associated family of conjugate lines. The two types of “discrete conjugate semi-geodesic nets” constitute discrete focal nets of circular nets, which mimics the classical connection between surfaces parametrized in terms of curvature coordinates and their focal surfaces on which one corresponding family of coordinate lines are geodesics. The discrete surfaces constructed in this manner are termed circular-geodesic and conical-geodesic nets, respectively, and may be characterized by compact angle conditions. Geometrically, circular-geodesic nets are constructed via normal lines of circular nets, while conical-geodesic nets inherit their name from their intimately related conical nets, which also discretize curvature line parametrized surfaces. We establish a variety of properties of these discrete nets, including their algebraic and geometric 3D consistency, with the latter playing an important role in (integrable) discrete differential geometry.
|

|
Tim Hoffmann, Martin Kilian, Katrin Leschke, and Francisco Martin, editors.
Minimal Surfaces: Integrable Systems and Visualisation, volume
349 of PROMS.
Springer, 2021.
[ bib ]
|
|
Alexander I. Bobenko, Tim Hoffmann, and Andrew O. Sageman-Furnas.
Compact bonnet pairs: isothermic tori with the same curvatures, 2021.
[ bib |
arXiv ]
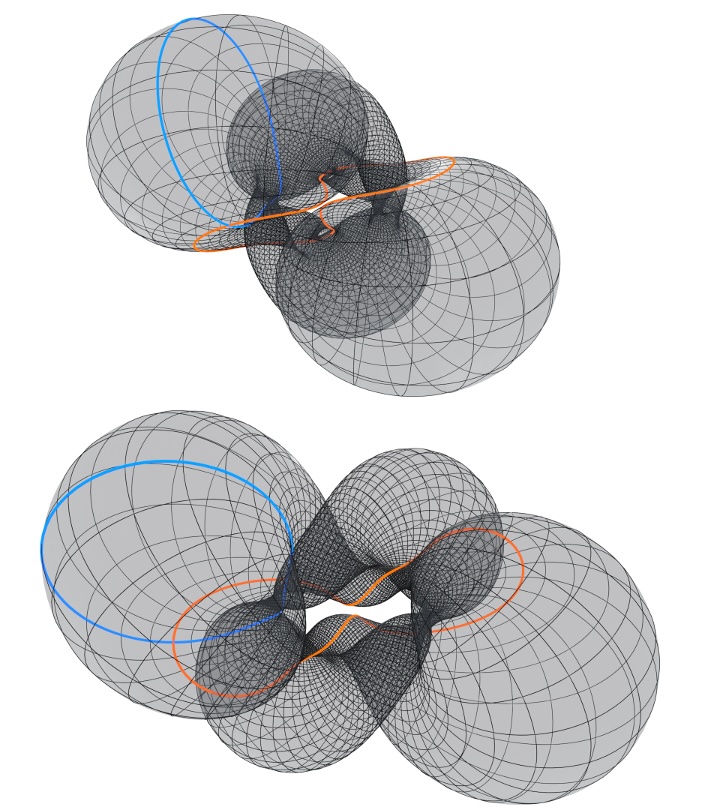
We explicitly construct a pair of immersed tori in three dimensional Euclidean space that are related by a mean curvature preserving isometry. These are the first examples of compact Bonnet pairs. This resolves a longstanding open problem on whether the metric and mean curvature function determine a unique compact surface.
We use the relationship between Bonnet pairs and isothermic surfaces. As a part of our construction we give a complete classification of isothermic surfaces with one family of planar curvature lines and of the corresponding cylinders.
|
|
Tim Hoffmann and Zi Ye.
A discrete extrinsic and intrinsic Dirac operator.
J. Exp. Math., 2020.
[ bib |
arXiv ]
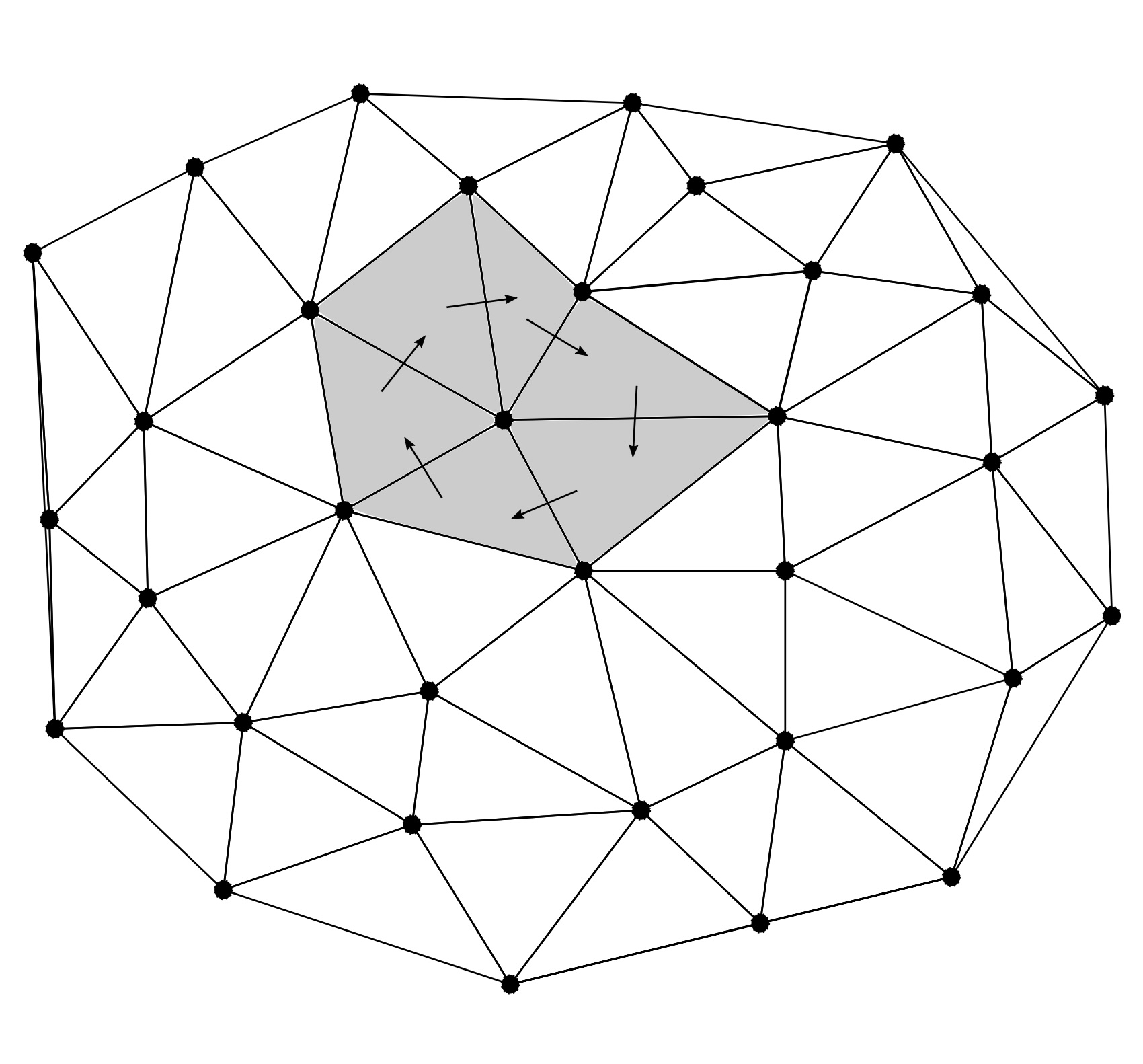
In differential geometry of surfaces the Dirac operator appears intrinsically as a tool to address the immersion problem as well as in an extrinsic flavour (that comes with spin transformations to comformally transfrom immersions) and the two are naturally related.
In this paper we consider a corresponding pair of discrete Dirac operators, the latter on discrete surfaces with polygonal faces and normals defined on each face, and show that many key properties of the smooth theory are preserved. In particular, the corresponding spin transformations, conformal invariants for them, and the relation between this operator and its intrinsic counterpart are discussed.
|
|
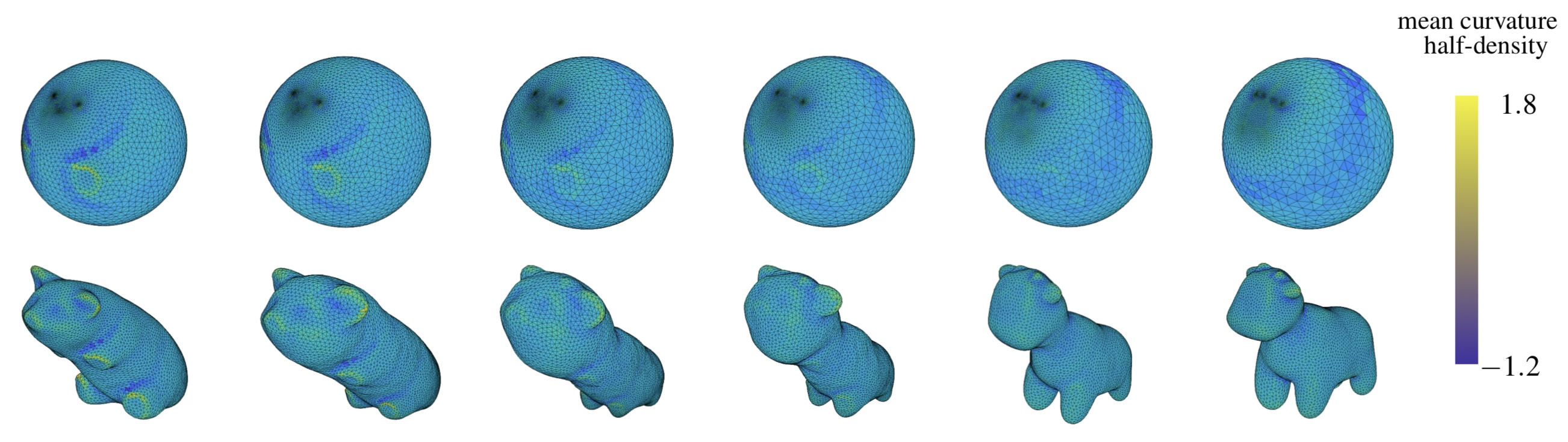
Z. Ye, Nobuyuki Umetani, Takeo Igarashi, and T. Hoffmann.
A curvature and density-based generative representation of shapes.
Computer Graphics Forum, 40, 10 2020.
[ bib |
DOI |
arXiv ]
This paper introduces a generative model for 3D surfaces based on a representation of shapes with mean curvature and metric, which are invariant under rigid transformation. Hence, compared with existing 3D machine learning frameworks, our model substantially reduces the influence of translation and rotation. In addition, the local structure of shapes will be more precisely captured, since the curvature is explicitly encoded in our model. Specifically, every surface is first conformally mapped to a canonical domain, such as a unit disk or a unit sphere. Then, it is represented by two functions: the mean curvature half-density and the vertex density, over this canonical domain. Assuming that input shapes follow a certain distribution in a latent space, we use the variational autoencoder to learn the latent space representation. After the learning, we can generate variations of shapes by randomly sampling the distribution in the latent space. Surfaces with triangular meshes can be reconstructed from the generated data by applying isotropic remeshing and spin transformation, which is given by Dirac equation. We demonstrate the effectiveness of our model on datasets of man-made and biological shapes and compare the results with other methods.
|

|
Michael Rabinovich, Tim Hoffmann, and Olga Sorkine-Hornung.
Modeling curved folding with freeform deformations.
ACM Transactions on Graphics (proceedings of ACM SIGGRAPH
ASIA), 38(6), 2019.
[ bib ]
We present a computational framework for interactive design and exploration of curved folded surfaces. In current practice, such surfaces are typically created manually using physical paper, and hence our objective is to lay the foundations for the digitalization of curved folded surface design. Our main contribution is a discrete binary characterization for folds between discrete developable surfaces, accompanied by an algorithm to simultaneously fold creases and smoothly bend planar sheets. We complement our algorithm with essential building blocks for curved folding deformations: objectives to control dihedral angles and mountain-valley assignments. We apply our machinery to build the first interactive freeform editing tool capable of modeling bending and folding of complicated crease patterns.
|

|
Michael Rabinovich, Tim Hoffmann, and Olga Sorkine-Hornung.
Discrete geodesic nets for modeling developable surfaces.
ACM Trans. Graph., 37(2):16:1--16:17, February 2018.
[ bib |
DOI |
arXiv ]
We present a discrete theory for modeling developable surfaces as quadrilateral meshes satisfying simple angle constraints. The basis of our model is a lesser known characterization of developable surfaces as manifolds that can be parameterized through orthogonal geodesics. Our model is simple, local, and, unlike previous works, it does not directly encode the surface rulings. This allows us to model continuous deformations of discrete developable surfaces independently of their decomposition into torsal and planar patches or the surface topology. We prove and experimentally demonstrate strong ties to smooth developable surfaces, including a theorem stating that every sampling of the smooth counterpart satisfies our constraints up to second order. We further present an extension of our model that enables a local definition of discrete isometry. We demonstrate the effectiveness of our discrete model in a developable surface editing system, as well as computation of an isometric interpolation between isometric discrete developable shapes.
Keywords: Discrete developable surfaces, discrete differential geometry, geodesic nets, isometry, mesh editing, shape interpolation, shape modeling
|

|
Michael Rabinovich, Tim Hoffmann, and Olga Sorkine-Hornung.
The shape space of discrete orthogonal geodesic nets.
ACM Transactions on Graphics (proceedings of ACM SIGGRAPH
ASIA), 37(6), 2018.
[ bib ]
Discrete orthogonal geodesic nets (DOGs) are a quad mesh analogue of developable surfaces. In this work we study continuous deformations on these discrete objects. Our main theoretical contribution is the characterization of the shape space of DOGs for a given net connectivity. We show that generally, this space is locally a manifold of a fixed dimension, apart from a set of singularities, implying that DOGs are continuously deformable. Smooth flows can be constructed by a smooth choice of vectors on the manifold's tangent spaces, selected to minimize a desired objective function under a given metric. We show how to compute such vectors by solving a linear system, and we use our findings to devise a geometrically meaningful way to handle singular points. We base our shape space metric on a novel DOG Laplacian operator, which is proved to converge under sampling of an analytical orthogonal geodesic net. We further show how to extend the shape space of DOGs by supporting creases and curved folds and apply the developed tools in an editing system for developable surfaces that supports arbitrary bending, stretching, cutting, (curved) folds, as well as smoothing and subdivision operations.
|
|
Zi Ye, Olga Diamanti, Chengcheng Tang, Leonidas Guibas, and Tim Hoffmann.
A unified discrete framework for intrinsic and extrinsic dirac
operators for geometry processing.
Computer Graphics Forum, 37:93--106, 08 2018.
[ bib |
DOI ]
Spectral mesh analysis and processing methods, namely ones that utilize eigenvalues and eigenfunctions of linear operators on meshes, have been applied to numerous geometric processing applications. The operator used predominantly in these methods is the Laplace‐Beltrami operator, which has the often‐cited property that it is intrinsic, namely invariant to isometric deformation of the underlying geometry, including rigid transformations. Depending on the application, this can be either an advantage or a drawback. Recent work has proposed the alternative of using the Dirac operator on surfaces for spectral processing. The available versions of the Dirac operator either only focus on the extrinsic version, or introduce a range of mixed operators on a spectrum between fully extrinsic Dirac operator and intrinsic Laplace operator. In this work, we introduce a unified discretization scheme that describes both an extrinsic and intrinsic Dirac operator on meshes, based on their continuous counterparts on smooth manifolds. In this discretization, both operators are very closely related, and preserve their key properties from the smooth case. We showcase various applications of our operators, with improved numerics over prior work.
|

|
Tim Hoffmann, Andrew O. Sageman-Furnas, and Max Wardetzky.
A discrete parametrized surface theory in R3.
International Mathematics Research Notices,
2017(14):4217--4258, 2017.
[ bib |
DOI |
arXiv ]
We present a 2×2 Lax representation for discrete circular nets of constant negative Gauß curvature. It is tightly linked to the 4D consistency of the Lax representation of discrete K-nets (in asymptotic line parametrization). The description gives rise to Bäcklund transformations and an associated family. All the members of that family -- although no longer circular -- can be shown to have constant Gauß curvature as well. Explicit solutions for the Bäcklund transformations of the vacuum (in particular Dini's surfaces and breather solutions) and their respective associated families are given.
Keywords: discrete differential geometry, discrete integrable systems, Bäcklund transformations, multidimensional consistency
|

|
Tim Hoffmann and Andrew O. Sageman-Furnas.
A 2x2 lax representation, associated family, and Baecklund
transformation for circular k-nets.
Discrete & Computational Geometry, 56(2):472--501, 2016.
[ bib |
DOI |
arXiv ]
We propose a discrete surface theory in 3 that unites the most prevalent versions of discrete special parametrizations. Our theory encapsulates a large class of discrete surfaces given by a Lax representation and, in particular, the one-parameter associated families of constant curvature surfaces. Our theory is not restricted to integrable geometries, but extends to a general surface theory.
|
|
A. I. Bobenko and T. Hoffmann.
S-conical cmc surfacea. towards a unified theory of discrete surfaces
with constant mean curvature.
In A. I. Bobenko, editor, Advances in Discrete Differential
Geometry, pages 287--308. Springer, 2016.
[ bib ]
We introduce a novel class of s-conical nets and, in particular, study s-conical nets with constant mean curvature. Moreover we give a unified description of nets of various types: circular, conical and s-isothermic. The later turn out to be interpolating between the circular net discretization and the s-conical one.
|
|
Tim Hoffmann, Wayne Rossman, Takeshi Sasaki, and Masaaki Yoshida.
Discrete flat surfaces and linear Weingarten surfaces in hyperbolic
3-space.
Transactions of the American Mathematical Society,
364(11):5605--5644, 2012.
[ bib |
arXiv ]
We define discrete flat surfaces in hyperbolic 3-space H3 from the perspective of discrete integrable systems and prove properties that justify the definition. We show how these surfaces correspond to previously defined discrete constant mean curvature 1 surfaces in H3, and we also describe discrete focal surfaces (discrete caustics) that can be used to define singularities on discrete flat surfaces. Along the way, we also examine discrete linear Weingarten surfaces of Bryant type in H3, and consider an example of a discrete flat surface related to the Airy equation that exhibits swallowtail singularities and a Stokes phenomenon.
|
|
Tim Hoffmann.
On local deformations of planar quad-meshes.
In Proceedings of the Third International Congress Conference on
Mathematical Software, ICMS'10, pages 167--169, Berlin, Heidelberg, 2010.
Springer-Verlag.
[ bib |
http ]
|
|
Tim Hoffmann.
A Darboux transformation for discrete s-isothermic surfaces.
Journal of Math-for-Industry, 2, 2010.
[ bib ]
We give an overview on the discretization of isothermic surfaces,
with special emphasis on the so-called s-isothermic surfaces, which
are in some sense a nonlinear deformation of the classical discrete
isothermic surfaces. For s-isothermic surfaces we give a way to define
surfaces of constant mean curvature (cmc surfaces for short) without
actually defining an a priori notion of curvature itself. We will
compute discrete versions of rotational symmetric cmc surfaces
(Delaunay surfaces) as an example. Finally, we give a discrete
equivalent of the Sinh-Gordon equation, solutions of which describe
-- in complete analogy to the smooth case -- discrete s-isothermic
cmc surfaces.
|

|
Steffen Weißmann, Charles Gunn, Peter Brinkmann, Tim Hoffmann, and Ulrich
Pinkall.
jreality: a java library for real-time interactive 3d graphics and
audio.
In MM '09: Proceedings of the seventeen ACM international
conference on Multimedia, pages 927--928, New York, NY, USA, 2009. ACM.
[ bib |
DOI ]
|
|
T. Hoffmann.
Discrete Differential Geometry of Curves and Surfaces,
volume 18 of MI Lecture Note Series.
Faculty of Mathematics, Kyushu University, 2009.
[ bib ]
|
|
W. K. Schief, A. I. Bobenko, and Hoffmann T.
On the integrability of infinitesimal and finite deformations of
polyhedral surfaces.
In Alexander I. Bobenko, John M. Sullivan, Peter Schröder, and
Günter M. Ziegler, editors, Discrete Differential Geometry,
volume 38 of Oberwolfach Seminars, pages 67--93. Birkhäuser Basel,
2008.
[ bib ]
It is established that there exists an intimate connection between isometric deformations of polyhedral surfaces and discrete integrable systems. In particular, Sauer's kinematic approach is adopted to show that second-order infinitesimal isometric deformations of discrete surfaces composed of planar quadrilaterals (discrete conjugate nets) are determined by the solutions of an integrable discrete version of Bianchi's classical equation governing finite isometric deformations of conjugate nets. Moreover, it is demonstrated that finite isometric deformations of discrete conjugate nets are completely encapsulated in the standard integrable discretization of a particular nonlinear σ-model subject to a constraint. The deformability of discrete Voss surfaces is thereby retrieved in a natural manner.
|

|
Tim Hoffmann.
Discrete Hashimoto surfaces and a doubly discrete smoke-ring flow.
In Alexander I. Bobenko, John M. Sullivan, Peter Schröder, and
Günter M. Ziegler, editors, Discrete Differential Geometry,
volume 38 of Oberwolfach Seminars, pages 95--115. Birhkäuser Basel,
2008.
[ bib |
arXiv ]
In this paper Bäcklund transformations for smooth and space discrete Hashimoto surfaces are discussed and a geometric interpretation is given. It is shown that the complex curvature of a discrete space curve evolves with the discrete nonlinear Schrödinger equation (NLSE) of Ablowitz and Ladik, when the curve evolves with the Hashimoto or smoke-ring flow. A doubly discrete Hashimoto flow is derived and it is shown that in this case the complex curvature of the discrete curve obeys Ablovitz and Ladik's doubly discrete NLSE. Elastic curves (curves that evolve by rigid motion under the Hashimoto flow) in the discrete and doubly discrete case are shown to be the same.
|
|
A. Bobenko, T. Hoffmann, and B. Springborn.
Minimal surfaces from circle patterns: Geometry from combinatorics.
Ann. Math., 164(1):231--264, 2006.
[ bib |
arXiv ]
We suggest a new definition for discrete minimal surfaces in terms of sphere packings with orthogonally intersecting circles. These discrete minimal surfaces can be constructed from Schramm's circle patterns. We present a variational principle which allows us to construct discrete analogues of some classical minimal surfaces. The data used for the construction are purely combinatorial--the combinatorics of the curvature line pattern. A Weierstrass-type representation and an associated family are derived. We show the convergence to continuous minimal surfaces.
|

|
T. Hoffmann and M. Schmies.
jreality, jtem, and oorange - a way to do math with computers.
In ICMS, volume 4151 of Lecture Notes in Computer
Science, pages 74--85. Springer, 2006.
[ bib |
http ]
|
|
T. Hoffmann and N. Kutz.
Discrete curves in CP1 and the Toda lattice.
Stud. Appl. Math., 113(1):31--55, 2004.
[ bib |
arXiv ]
In this paper we investigate flows on discrete curves in 2, 1, , and 2. A novel interpretation of the one dimensional Toda lattice hierachy and reductions thereof as flows on discrete curves will be found.
|
|
A. I. Bobenko and T. Hoffmann.
Hexagonal circle patterns and integrable systems. patterns with
constant angles.
Duke Math. J., 116(3), 2003.
[ bib |
arXiv ]
Hexagonal circle patterns with constant intersection angles are introduced and stud- ied. It is shown that they are described by discrete integrable systems of Toda type. Conformally symmetric patterns are classified. Circle pattern analogs of holomorphic mappings zc and log z are constructed as special isomonodromic solutions. Circle patterns studied in the paper include Schramm's circle patterns with the combina- torics of the square grid as a special case.
|

|
Tim Hoffmann.
jDvi -- a way to put interactive TeX on the web.
In Multimedia Tools for Communicating Mathematics,
pages 117--130. Springer-Verlag, Berlin, Heidelberg, 2002.
[ bib ]
|
|
A. I. Bobenko, T. Hoffmann, and Suris Yu. B.
Hexagonal circle patterns and integrable systems. patterns with the
multi-ratio property and lax equations on the regular triangular lattice.
Int. Math. Res. Notices, 3:111--164, 2002.
[ bib |
arXiv ]
Hexagonal circle patterns are introduced, and a subclass thereof is studied in detail. It is characterized by the following property: For every circle the multi-ratio of its six intersection points with neighboring circles is equal to −1. The relation of such patterns with an integrable system on the regular triangular lattice is established. A kind of a B ̈acklund transformation for circle patterns is studied. Further, a class of isomonodromic solutions of the aforementioned integrable system is introduced, including circle patterns analogs to the analytic functions zα and log z.
|
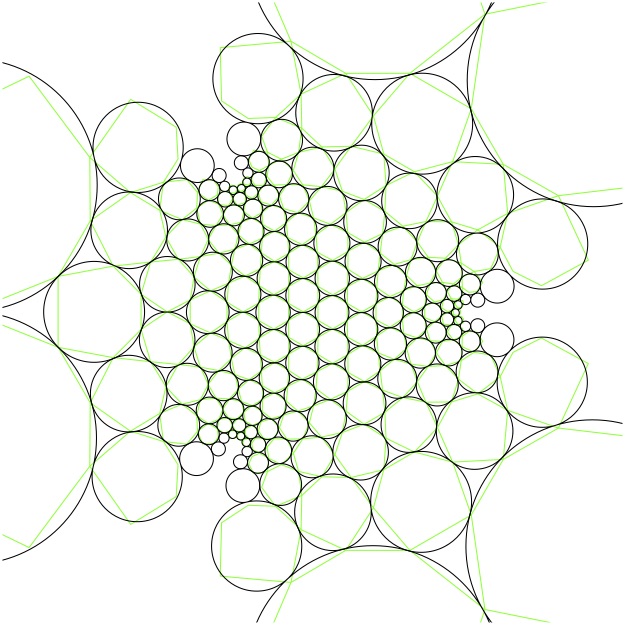
|
A. Bobenko and T. Hoffmann.
Conformally symmetric circle packings. a generalization of Doyle
spirals.
J. Exp. Math., 10(1), 2001.
[ bib |
arXiv ]
From the geometric study of the elementary cell of hexagonal circle packings---a flower of 7 circles---the class of conformally symmetric circle packings is defined. Up to Möbius transformations, this class is a three parameter family, that contains the famous Doyle spirals as a special case. The solutions are given explicitly. It is shown that these circle packings can be viewed as descretization s of the quotient of two Airy functions. The online version of this paper contains Java applets that let you experiment with the circle packings directly.
|

|
T. Hoffmann.
Discrete curves and surfaces.
PhD thesis, Technische Universität Berlin, 2000.
[ bib |
.pdf ]
|

|
T. Hoffmann.
On the equivalence of the discrete nonlinear Schrödinger
equation and the discrete isotropic Heisenberg magnet.
Phys Lett. A, 265(1--2):62--67, 2000.
[ bib ]
The equivalence of the discrete isotropic Heisenberg magnet (IHM) model and the discrete nonlinear Schrödinger equation (NLSE) given by Ablowitz and Ladik is shown. This is used to derive the equivalence of their discretization with the one by Izergin and Korepin. Moreover a doubly discrete IHM is presented that is equivalent to Ablowitz' and Ladiks doubly discrete NLSE.
|

|
T. Hoffmann, J. Kellendonk, N. Kutz, and N. Reshetikhin.
Factorization dynamics and Coxeter-Toda lattices.
Comm. Math. Phys., 212(2):297--321, 2000.
[ bib |
arXiv ]
It is shown that the factorization relation on simple Lie groups with standard Poisson Lie structure restricted to Coxeter symplectic leaves gives an integrable dynamical system. This system can be regarded as a discretization of the Toda flow. In case of SL n the integrals of the factorization dynamics are integrals of the relativistic Toda system. A substantial part of the paper is devoted to the description of symplectic leaves in simple complex Lie groups, its Borel subgroups and their doubles.
|

|
T. Hoffmann.
Rauchringe in der mathematik/smoke rings in mathmatics.
International forum man and architecture, 27/28, 1999.
[ bib ]
|

|
U. Hertrich-Jeromin, T. Hoffmann, and Pinkall U.
A discrete version of the Darboux transform for isothermic
surfaces.
In A. Bobenko and R. Seiler, editors, Discrete integrable
geometry and physics, pages 59--81. Oxford University Press, 1999.
[ bib |
arXiv ]
|

|
T. Hoffmann.
Discrete cmc surfaces and discrete holomorphic maps.
In A. Bobenko and R. Seiler, editors, Discrete integrable
geometry and physics, pages 97--112. Oxford University Press, 1999.
[ bib ]
|

|
T. Hoffmann.
Discrete amsler surfaces and a discretePainlevé III equation.
In A. Bobenko and R. Seiler, editors, Discrete integrable
geometry and physics, pages 83--96. Oxford University Press, 1999.
[ bib ]
|

|
T. Hoffmann.
Discrete rotational cmc surfaces and the elliptic billiard.
In H.-C. Hege and K. Polthier, editors, Mathematical
Visualisation, pages 117--124. Springer, 1998.
[ bib ]
|









































